Thuật Toán Two Pointers - Cách Tiếp Cận Hiệu Quả Cho Developer Mới Bắt Đầu

Trong lập trình thuật toán, phương pháp "Two Pointers" là một cách tiếp cận tối ưu giúp giải quyết nhiều bài toán trên mảng và chuỗi với độ phức tạp thấp hơn so với cách thông thường. Đây là một kỹ thuật quan trọng được sử dụng rộng rãi trong các thuật toán tìm kiếm, sắp xếp và xử lý dữ liệu.

1. Two Pointers là gì?

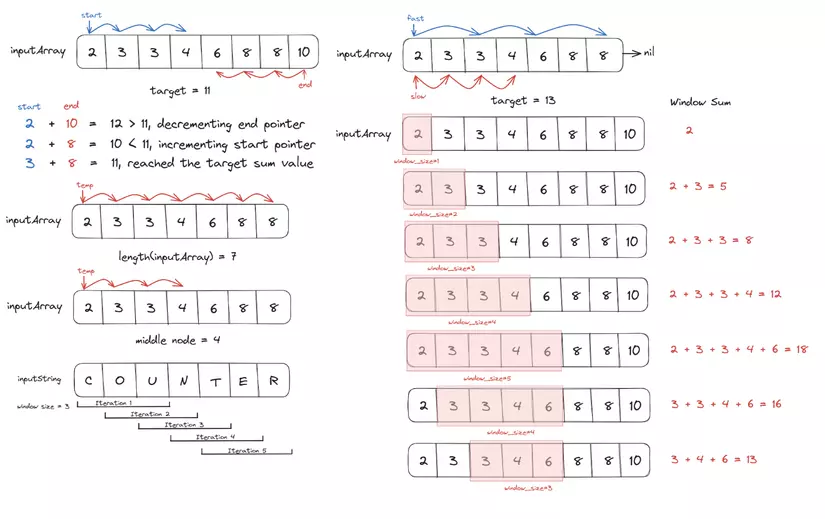
"Two Pointers" là một kỹ thuật trong đó ta sử dụng hai con trỏ để duyệt qua một cấu trúc dữ liệu như mảng hoặc danh sách liên kết. Hai con trỏ này có thể:

• Di chuyển về cùng một hướng (ví dụ: tìm khoảng con có tổng lớn nhất)
• Di chuyển về hai hướng ngược nhau (ví dụ: tìm hai số có tổng bằng một giá trị cố định)
• Di chuyển theo điều kiện cụ thể (ví dụ: thuật toán Merge Sort hoặc Binary Search)

2. Ứng dụng phổ biến

2.1. Tìm cặp số có tổng bằng một giá trị

Cho một mảng đã được sắp xếp, ta cần tìm hai số có tổng bằng target.

Giải pháp với Two Pointers:

• Đặt một con trỏ left ở đầu mảng và right ở cuối mảng.
• Nếu tổng của hai phần tử tại left và right lớn hơn target, ta giảm right.
• Nếu tổng nhỏ hơn target, ta tăng left.
• Lặp lại quá trình cho đến khi tìm thấy cặp số phù hợp hoặc left >= right.

Mã nguồn Python:

def two_sum_sorted(arr, target):
    left, right = 0, len(arr) - 1
    while left < right:
        current_sum = arr[left] + arr[right]
        if current_sum == target:
            return (arr[left], arr[right])
        elif current_sum < target:
            left += 1
        else:
            right -= 1
    return None

arr = [1, 2, 3, 4, 6]
target = 6
print(two_sum_sorted(arr, target))  # Output: (2, 4)

Độ phức tạp: O(N), nhanh hơn so với giải pháp brute-force O(N²).

2.2. Merge hai mảng đã sắp xếp (Merge Sort)

Trong thuật toán Merge Sort, kỹ thuật Two Pointers được sử dụng để hợp nhất hai mảng con đã được sắp xếp.

Giải pháp:

• Sử dụng hai con trỏ để lần lượt duyệt qua từng phần tử của hai mảng.
• So sánh phần tử hiện tại của hai mảng và đưa phần nhỏ hơn vào mảng kết quả.
• Tiếp tục cho đến khi duyệt hết một trong hai mảng, sau đó sao chép các phần tử còn lại vào mảng kết quả.

Mã nguồn Python:

def merge_sorted_arrays(arr1, arr2):
    i, j = 0, 0
    merged = []
    while i < len(arr1) and j < len(arr2):
        if arr1[i] < arr2[j]:
            merged.append(arr1[i])
            i += 1
        else:
            merged.append(arr2[j])
            j += 1
    merged.extend(arr1[i:])
    merged.extend(arr2[j:])
    return merged

arr1 = [1, 3, 5]
arr2 = [2, 4, 6]
print(merge_sorted_arrays(arr1, arr2))  # Output: [1, 2, 3, 4, 5, 6]

Độ phức tạp: O(N + M) (tốt hơn so với cách nối mảng rồi sắp xếp O((N+M) log(N+M))).

2.3. Tìm phần tử trong mảng bằng Binary Search

Binary Search là một ví dụ khác của kỹ thuật Two Pointers khi ta sử dụng hai con trỏ (low và high) để thu hẹp phạm vi tìm kiếm trong mỗi vòng lặp.

Mã nguồn Python:

def binary_search(arr, target):
    low, high = 0, len(arr) - 1
    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1
    return -1

arr = [1, 2, 3, 4, 6]
target = 4
print(binary_search(arr, target))  # Output: 3

Độ phức tạp: O(log N) do mỗi lần giảm nửa phạm vi tìm kiếm.

2.4. Kiểm tra chuỗi Palindrome

Kỹ thuật Two Pointers có thể dùng để kiểm tra xem một chuỗi có phải là palindrome (đọc xuôi và ngược giống nhau) hay không.

Giải pháp với Two Pointers:

• Đặt một con trỏ left ở đầu chuỗi và right ở cuối chuỗi.
• So sánh ký tự tại left và right.
• Nếu hai ký tự không khớp, chuỗi không phải là palindrome.
• Nếu khớp, tiếp tục di chuyển left lên và right xuống.
• Dừng lại khi left >= right.

Mã nguồn Python:

def is_palindrome(s):
    left, right = 0, len(s) - 1
    while left < right:
        if s[left] != s[right]:
            return False
        left += 1
        right -= 1
    return True

s = "racecar"
print(is_palindrome(s))  # Output: True

Độ phức tạp: O(N), nhanh hơn so với cách sử dụng chuỗi đảo ngược O(N).

3. Khi nào sử dụng Two Pointers?

• Khi cần tìm kiếm hoặc so sánh phần tử trong mảng đã sắp xếp.
• Khi xử lý các bài toán liên quan đến chuỗi hoặc danh sách liên kết.
• Khi có thể tận dụng việc duyệt một mảng theo cách tối ưu hơn O(N²) hoặc O(N log N).
• Khi cần tìm khoảng con liên tục có tổng lớn nhất (Sliding Window).
• Khi xử lý các bài toán về sắp xếp lại mảng theo điều kiện cụ thể (ví dụ: đưa các số chẵn lên trước, số lẻ về sau).
• Khi cần loại bỏ các phần tử trùng lặp trong danh sách liên kết mà không dùng thêm bộ nhớ.

4. Tổng kết

Kỹ thuật Two Pointers là một phương pháp mạnh mẽ giúp giải quyết nhiều bài toán tối ưu hơn so với brute-force. Nó được sử dụng rộng rãi trong các bài toán tìm kiếm, sắp xếp và xử lý mảng. Là một developer mới bắt đầu, bạn nên nắm vững kỹ thuật này để viết code hiệu quả hơn!

Hy vọng bài viết này giúp bạn hiểu rõ hơn về "Two Pointers" và cách áp dụng nó trong thực tế. Chúc bạn học tốt và code hiệu quả!