I. Đặt vấn đề

Trong các bài toán lập trình thi đấu, những câu hỏi về truy vấn đáp án trên một đoạn của dãy số là một trong những nội dung phổ biến và rất phong phú. Chúng ta đã được biết đến một dạng câu hỏi như vậy, đó chính là truy vấn cập nhật đoạn tăng theo hằng số (xem lại tại đây). Một ví dụ đơn giản khác của dạng câu hỏi này là tìm chỉ số của phần tử nhỏ nhất trong đoạn vị trí $[i, j]$ của một dãy số, còn được biết đến là bài toán RMQ. Lấy ví dụ, với mảng $A = [18, 17, 13, 19, 15, 11, 20];$ ta sẽ có $RMQ(1, 3) = 3$ - bởi vì phần tử $A[3]$ có giá trị nhỏ nhất trong các phần tử $A[1], A[2], A[3]$. Hoàn toàn tương tự, ta có $RMQ(3, 4) = 3, RMQ(1, 1) = 1, RMQ(1, 7) = 6, \dots$

Trong bài viết này, chúng ta sẽ cùng tìm hiểu một cấu trúc dữ liệu rất hiệu quả để giải quyết các truy vấn phạm vi động - có nghĩa là cần tìm đáp án trên nhiều phạm vi khác nhau của cùng một dãy số, ngoài ra dữ liệu trong phạm vi đó có thể bị thay đổi liên tục. Cấu trúc dữ liệu ta đang nói đến là Segment Tree (hay Interval Tree) - một ứng dụng của cây nhị phân dùng để lưu trữ thông tin của các đoạn trên dãy. Bài toán RMQ sẽ được sử dụng làm bài toán ví dụ để minh họa cho cấu trúc dữ liệu này. Phát biểu bài toán như sau:

Cho dãy số $A$ gồm $n$ phần tử $a_1, a_2, \dots, a_n$. Bạn cần trả lời $Q$ truy vấn, mỗi truy vấn thuộc hai loại:

• $1 \ x \ y$: Gán giá trị $y$ cho phần tử ở vị trí $x$.
• $2 \ l \ r$: Đưa ra giá trị của phần tử nhỏ nhất trong đoạn vị trí $[l, r]$ của dãy số.

Input:

• Dòng đầu tiên gồm hai số nguyên $n$ và $Q$ - độ dài dãy số và số lượng truy vấn.
• Dòng thứ hai chứa $n$ số nguyên $a_1, a_2, \dots, a_n$ phân tách nhau bởi dấu cách.
• $Q$ dòng tiếp theo, mỗi dòng chứa ba số nguyên dương thể hiện một truy vấn.

Ràng buộc:

• $1 \le n, Q \le 10^5$.
• $1 \le a_i \le 10^9; \forall i: 1 \le i \le n$.
• $1 \le x \le n$.
• $1 \le y \le 10^9$.
• $1 \le l \le r \le n$.

Output:

• Ứng với mỗi truy vấn loại $2,$ in ra đáp án trên một dòng.

Sample Input:

7 4
18 17 13 19 15 11 20
1 3 15
2 3 4
1 1 9
2 1 7

Sample Output:

15
9

II. Sử dụng Cây phân đoạn

1. Từ giải pháp Chia để trị...

Trước hết, ta cùng xét một giải pháp chia để trị để giải bài toán RMQ:

• Nếu dãy đang xét chứa một phần tử, thì bản thân phần tử đó là giá trị nhỏ nhất trong dãy đó.
• Nếu không, ta chia dãy đó thành hai dãy con liên tiếp nhỏ hơn, mỗi dãy con gần bằng một nửa kích thước của dãy ban đầu, và tìm giá trị nhỏ nhất tương ứng của chúng. Giá trị nhỏ nhất của dãy ban đầu chính là giá trị nhỏ hơn giữa hai giá trị nhỏ nhất của các dãy con.

Hình vẽ dưới đây mô tả giải pháp chia để trị với mảng $A = [9, 2, 6, 3, 1, 5, 7]$:

<center>

</center>

Với cách chia đoạn như vậy, kể cả khi phát sinh thao tác sửa đổi một phần tử nào đó trên mảng, thì ta cũng chỉ cần cập nhật lại kết quả ở một số đoạn nhất định. Chẳng hạn nếu như sửa phần tử $A[5]$ thành $8,$ thì ta chỉ cần cập nhật lại các đoạn $[1, 7], [5, 7], [5, 6]$ và $[5, 5]$:

<center>

</center>

Tổng quát lại, gọi $a_i$ là phần tử thứ $i$ trong mảng, thì việc xác định $RMQ(l, r)$ có thể viết dưới dạng hàm đệ quy như sau:

$$RMQ(l, r) = \begin{cases}a_l; \text{nếu } l = r.\\ \text{min}\bigg(RMQ\left(l, \left\lfloor{\frac{l + r}{2}} \right\rfloor\right), RMQ\left(\left\lfloor{\frac{l + r}{2}} \right\rfloor + 1, r\right)\bigg); \text{nếu } l < r. \end{cases}$$

Và khi cần sửa đổi một phần tử $a_i$ trong mảng, thì ta chỉ cần tính lại các $RMQ(l, r)$ với $l \le i \le r$.

2. ...tới cấu trúc dữ liệu Cây phân đoạn

Sau khi có được định nghĩa hàm đệ quy trên, giả sử ta gọi $RMQ(1, n)$ với $n$ là kích thước của dãy số để tính được phần tử nhỏ nhất của dãy. Nhận xét như sau: Hàm đệ quy $RMQ(1, n)$ sẽ có hai "con" là $RMQ\Big(1, \left\lfloor{\frac{n + 1}{2}}\right\rfloor\Big)$ và $RMQ\Big(\left\lfloor{\frac{n + 1}{2}}\right\rfloor + 1, n\Big)$ theo lời gọi đệ quy, rồi hai con này lại tiếp tục có hai con nữa,...cứ như vậy cho tới khi đạt đến trường hợp cơ sở là $l = r$.

Nếu như biểu diễn các hàm đệ quy này bằng một cấu trúc cây, thì hàm $RMQ(1, n)$ sẽ là gốc, mỗi nút sẽ có thêm hai con nữa,...các trường hợp cơ sở sẽ là lá của cây. Khi đó, cấu trúc cây gọi đệ quy của hàm $RMQ$ chính là cấu trúc Cây phân đoạn. Các thao tác lấy kết quả, cập nhật lại phần tử sẽ là các thao tác được hỗ trợ trên cấu trúc dữ liệu này (sẽ được nói chi tiết tiếp sau đây).

Lấy ví dụ, với mảng $A = [9, 2, 6, 3, 1, 5, 7]$ thì cây phân đoạn kiểm soát thông tin các đoạn trên mảng sẽ được mô tả như sau:

<center>

</center>

3. Cấu trúc một Cây phân đoạn

Từ những điều đã nói ở trên, sau đây chúng ta có thể xác định được cấu trúc của Cây phân đoạn như sau:

• Cây phân đoạn là một Cây nhị phân đầy đủ (mỗi nút hoặc là lá, hoặc có đủ hai nút con).
• Mỗi nút quản lý một dãy các đối tượng liên tiếp, trong nút chứa thông tin tổng hợp từ các đối tượng mà nó quản lý.
• Với một dãy gồm $n$ phần tử, nút gốc quản lý các đối tượng từ $1$ tới $n$.
• Nếu một nút quản lý dãy các đối tượng từ $l$ tới $r \ (l<r)$ thì nút con trái của nó quản lý các đối tượng từ $l$ tới $mid$ và nút con phải của nó quản lý các đối tượng từ $mid+1$ tới $r$ $\Big($với $mid=\left\lfloor{\frac{l + r}{2}}\right\rfloor\Big)$.
• Nếu một nút chỉ quản lý một đối tượng thì nó sẽ là nút lá và không có nút con.
• Chiều cao của cây phân đoạn là $O(\log n),$ bởi vì khi đi xuống từ gốc đến lá, kích thước của mỗi đoạn giảm đi một nửa.
• Tại mỗi độ sâu của cây, không có phần tử nào được quản lý bởi $2$ nút khác nhau của cây.

4. Các thao tác trên Cây phân đoạn

Xây dựng cây

Muốn lấy thông tin và cập nhật các phần tử trên dãy, thì trước tiên chúng ta phải xây dựng một cây phân đoạn lưu thông tin ban đầu của dãy số.

Lấy bài toán ban đầu làm ví dụ, ta sẽ cần phải quyết định hai điều sau:

1. Thông tin được lưu trữ trong các nút của cây. Vì cây phân đoạn này lưu chỉ số của phần tử có giá trị nhỏ nhất, nên mỗi nút sẽ lưu chỉ số của phần tử nhỏ nhất trong đoạn $[l, r]$ mà nó quản lý.
2. Phép toán hợp nhất thông tin từ hai nút con của cây lên nút cha. Vì cây hiện tại lưu giá trị nhỏ nhất, nên thông tin từ hai nút con quản lý hai đoạn $[l_1, r_1]$ và $[l_2, r_2]$ sẽ được hợp nhất thành thông tin của nút cha tương ứng với đoạn $[l_1, r_2]$ bằng cách lấy $\text{min}$ của hai nút con.

Lưu ý rằng, riêng với các nút là lá của cây, thì thông tin lưu trên đó sẽ là thông tin của một phần tử (đoạn độ dài $1$). Ví dụ trong bài toán này, các đỉnh lá sẽ lưu giá trị $a_i$ tương ứng mà nó quản lý.

Để xây dựng một cây phân đoạn, ta có thể chọn một trong hai cách: Xây dựng từ dưới lên trên hoặc từ trên xuống dưới. Tuy nhiên, trong bài viết này sẽ trình bày cách xây dựng từ trên xuống dưới, vì nó dễ hiểu hơn. Cách xây dựng này dựa trên mô hình đệ quy như sau:

• Bắt đầu từ đỉnh gốc, ta di chuyển tới các đỉnh con cho tới khi xuống tới lá:
  • Nếu nút đang xét là nút lá, thì trả ngay về giá trị tương ứng trên mảng mà nút đó đang lưu trữ (trường hợp cơ sở).
  • Ngược lại, nếu nút đang xét không phải là nút lá, ta gọi đệ quy để tính toán giá trị của hai nút con. Sau khi hai lệnh gọi đệ quy được thực hiện, giá trị của nút đang xét sẽ bằng giá trị được "hợp nhất" từ hai nút con.
• Thủ tục đệ quy bắt đầu từ đỉnh gốc, do đó ta sẽ tính toán được giá trị cho mọi nút trên cây phân đoạn.

Cập nhật thông tin

Giờ, nếu như phát sinh truy vấn sửa đổi phần tử trong mảng, chẳng hạn gán $a_i = x$ thì cây phân đoạn phải được cập nhật lại tương ứng với mảng đã sửa đổi.

Trước tiên, ta cần sửa đổi nút lá tương ứng với phần tử bị thay đổi (các nút lá khác thì không bị ảnh hưởng). Từ đó, nút cha của nút bị thay đổi cũng sẽ bị ảnh hưởng, và tương tự với toàn bộ các nút tổ tiên cho tới tận nút gốc, vì đoạn của các nút đó quản lý cũng chứa nút bị thay đổi. Tức là, toàn bộ các nút nằm trên đường đi đơn từ nút gốc tới nút lá tương ứng sẽ bị thay đổi, còn các nút khác không bị ảnh hưởng. Do đó, với một dãy gồm $n$ phần tử, thì chỉ có tối đa $\log_2(n)$ nút cần cập nhật, vì độ cao của cây nhị phân tương ứng là $\log_2(n)$.

Lấy ví dụ, với mảng $A = [9, 2, 6, 3, 1, 5, 7]$ và phần tử $A[5]$ thay đổi từ $1$ thành $8,$ thì cây phân đoạn quản lý giá trị nhỏ nhất của mảng $A$ sẽ cập nhật lại như sau:

<center>

</center>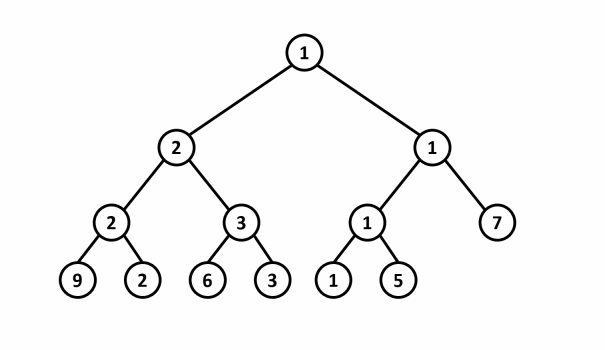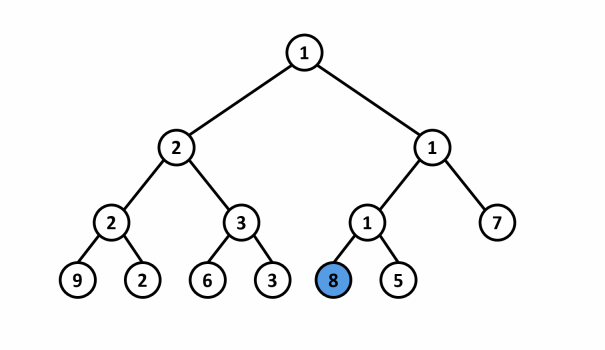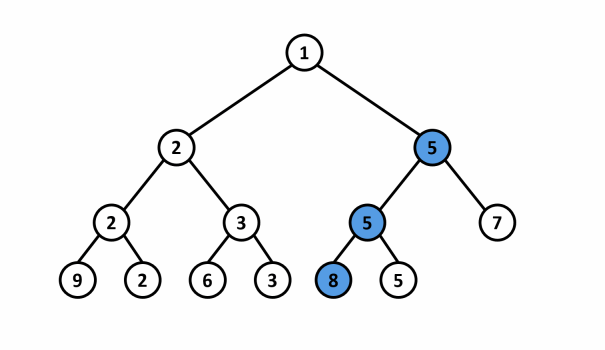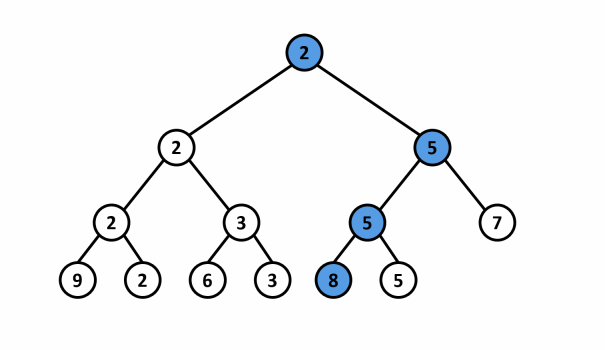

Thao tác cập nhật có thể được xây dựng bởi một hàm đệ quy như sau:

• Ta bắt đầu từ nút gốc; điều này dẫn đến lệnh gọi đệ quy tới một nút con quản lí đoạn chứa phần tử cần sửa đổi (nút con còn lại và cây con của nó không bị ảnh hưởng), v.v…Cho đến trường hợp cơ sở là nút lá được liên kết với phần tử cần cập nhật, ta sửa lại giá trị của nút lá đó.
• Sau khi hoàn tất lệnh gọi đệ quy cho các nút con (trừ trường hợp cơ sở), giá trị của nút đang xét sẽ được cập nhật lại theo giá trị hai nút con của nó.

Lấy giá trị

Thao tác lấy giá trị trên cây phân đoạn sử dụng để lấy ra thông tin của một đoạn trên dãy. Trong bài toán đang xét, ta cần trả lời truy vấn tìm giá trị nhỏ nhất trong đoạn $[l, r]$ của dãy số.

Để dễ hình dung, ta lấy một ví dụ như sau: Xét dãy $A = [9, 2, 6, 3, 1, 5, 7]$ và ta cần biết phần tử nhỏ nhất trong đoạn $[1, 6]$ của dãy. Cây phân đoạn đã được xây dựng như hình dưới đây:

<center>

</center>

Gọi $RMQ(l, r)$ là phần tử có giá trị nhỏ nhất trong đoạn $[l, r]$. Trên cây phân đoạn, mỗi nút đều quản lý một đoạn nào đó, tuy nhiên, không phải đoạn nào cũng được quản lý. Chẳng hạn như nút gốc chứa $RMQ(1, 7),$ nút con bên trái là $RMQ(1, 4),$ bên phải là $RMQ(5, 7),...$tuy nhiên không có nút nào chứa $RMQ(1, 6)$. Tuy nhiên, trên cây có những nút chứa các phần tử trong đoạn đó, chính là $RMQ(1, 4)$ và $RMQ(5, 6)$ (các nút màu xanh dương). Vì thế, ta có thể tính $RMQ(1, 6) = \text{min}\big(RMQ(1, 4), RMQ(5, 6)\big)$.

Ta có: $RMQ(x, y) = \text{min}\big(RMQ(x, z), RMQ(z + 1, y)\big)$ với $x \le z < y$. Vì thế, ta cần xác định một tập gồm ít nút nhất trên cây, sao cho tất cả phạm vi mà các nút đó quản lý, khi gộp lại sẽ đúng bằng đoạn đang cần truy vấn. Đó chính là đáp án mà ta đang tìm kiếm.

Để làm như vậy, ta sẽ bắt đầu từ gốc và đệ quy qua các nút mà phạm vi quản lí của nó có ít nhất một phần tử chung với đoạn cần truy vấn.

Trong ví dụ trên với $RMQ(1,6),$ xét hai nút con của gốc, ta nhận thấy rằng cả nút con bên trái và bên phải đều quản lí một số các phần tử con thuộc đoạn cần truy vấn $\big($đoạn $[1,6]\big)$. Do đó, ta sẽ thực hiện lệnh gọi đệ quy trên cả hai nút con của nút gốc. Khi đó, nút con bên trái của gốc đóng vai trò như một trường hợp cơ sở, vì phạm vi quản lí của nó được chứa hoàn toàn bên trong đoạn truy vấn; vậy nên nó được chọn (đánh dấu bằng màu xanh dương).

Còn với nút con bên phải của gốc $\big($nút chứa $RMQ(5,7)\big)$; ta nhận thấy rằng nút con bên trái của nút $RMQ(5,7),$ tức là $RMQ(5,6)$ có quản lí một số các phần tử con thuộc đoạn cần truy vấn, nhưng nút con bên phải là $RMQ(7,7)$ thì không. Vì vậy, ta chỉ tiếp tục gọi đệ quy trên nút con bên trái là nút chứa $RMQ(5,6)$ và bỏ qua không gọi đệ quy nút con bên phải là nút chứa $RMQ(7,7)$.

Khi đấy, nút con bên trái đó - nút $RMQ(5, 6)$ - sẽ là một trường hợp cơ sở khác, nó cũng được chọn (và đánh dấu bằng màu xanh dương).

Đệ quy kết thúc và giá trị nhỏ nhất của đoạn cần truy vấn chính là giá trị nhỏ nhất của các nút đã được chọn.

5. Cài đặt

Để lưu trữ một cây, có thể sử dụng tới danh sách liên kết, hoặc tạo ra một cấu trúc cây và danh sách cạnh, tuy nhiên điều này không hợp lý vì sẽ phải lưu trữ rất nhiều thông tin dư thừa.

Thay vào đó, ta sẽ lưu thông tin của từng nút vào một mảng. Thông tin của nút gốc sẽ đặt ở chỉ số thứ $1,$ thông tin của hai nút con lưu ở hai chỉ số $2$ và $3,$ thông tin của các nút con của các nút con đó lưu ở các chỉ số từ $4$ tới $7,...$Và ta có công thức sau: Nút có chỉ số $id$ thì con bên trái của nó được lưu ở chỉ số $2 \times id$ và con bên phải được lưu ở chỉ số $2 \times id + 1$.

Lấy một ví dụ minh họa, vẫn là mảng $A = [9, 2, 6, 3, 1, 5, 7];$ thì mảng biểu diễn cây phân đoạn lưu giá trị nhỏ nhất của mảng $A$ sẽ là mảng $st = [1,2,1,2,3,1,7,9,2,6,3,1,5]$. Hình vẽ dưới đây sẽ minh họa rõ hơn (các chỉ số màu đỏ thể hiện vị trí trên mảng của các nút):

<center>

</center>

Như vậy, coi như ta không cần phải tạo ra nguyên một cấu trúc cây, mà chỉ cần lưu trữ thông tin của các nút ở trên mảng (việc nó là cây sẽ tự hiểu một cách ngầm định). Giờ thì việc cài đặt trở nên dễ dàng hơn rất nhiều!

Quay trở lại bài toán ví dụ, ta cần giải quyết hai loại truy vấn:

• Truy vấn $1 \ x \ y$: Cập nhật phần tử $a_x = y$.
• Truy vấn $2 \ l \ r$: In ra phần tử nhỏ nhất trong đoạn $[l, r]$ của mảng.

Cách làm đơn giản nhất là với truy vấn $1,$ ta gán trực tiếp $a_x = y,$ còn với truy vấn $2$ thì sử dụng một vòng lặp để tìm ra kết quả. Dễ nhận thấy, với ràng buộc kích thước mảng là $10^5$ và số truy vấn cũng lên tới $10^5,$ phương pháp trên không thể đáp ứng thời gian chạy.

Ta sẽ sử dụng Segment Tree để giải quyết bài toán này như dưới đây:

#include <bits/stdc++.h>

using namespace std;

// Thủ tục xây dựng cây phân đoạn
void build_tree(int id, int l, int r, vector < int > &st, vector < int > &a) 
{
    // Đoạn chỉ gồm 1 phần tử, không có nút con.
    if (l == r) 
    {
        st[id] = a[l];
        return;
    }

    // Gọi đệ quy để xử lý các nút con của nút id.
    int mid = (l + r) >> 1; // (l + r) / 2
    build_tree(2 * id, l, mid, st, a);
    build_tree(2 * id + 1, mid + 1, r, st, a);
    
    // Cập nhật lại giá trị min của đoạn [l, r] theo 2 nút con.
    st[id] = min(st[2 * id], st[2 * id + 1]);
}

// Thủ tục cập nhật
void update(int id, int l, int r, int i, int val, vector < int > &st) 
{
    // Vị trí i nằm ngoài đoạn [l, r], ta bỏ qua nút id.
    if (l > i || r < i) 
        return;
    
    // Đoạn chỉ gồm 1 phần tử, không có nút con.
    if (l == r) 
    {
        st[id] = val;
        return;
    }
    
    // Gọi đệ quy để xử lý các nút con của nút id
    int mid = (l + r) >> 1; // (l + r) / 2
    update(2 * id, l, mid, i, val, st);
    update(2 * id + 1, mid + 1, r, i, val. st);
    
    // Cập nhật lại giá trị min của đoạn [l, r] theo 2 nút con.
    st[id] = min(st[2 * id], st[2 * id + 1]);
}


// Hàm lấy giá trị của đoạn [l, r].
int get(int id, int l, int r, int u, int v, vector < int > &st) 
{
    // Đoạn [u, v] không giao với đoạn [l, r], ta bỏ qua đoạn này.
    if (l >  v || r <  u) 
        return inf; 
    
    // Đoạn [l, r] nằm hoàn toàn trong đoạn [u, v] mà ta đang truy vấn, 
    // ta trả lại thông tin lưu ở nút id.
    if (l >= u && r <= v) 
        return st[id];

    // Gọi đệ quy với các nút con của nút id
    int mid = l + r >> 1; // (l + r) / 2
    int get1 = get(2 * id, l, mid, u, v, st);
    int get2 = get(2 * id + 1, mid + 1, r, u, v, st);
    
    // Trả ra giá trị nhỏ nhất của đoạn hiện tại theo 2 nút con.
    return min(get1, get2);
}

int main() 
{
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
	
    int n;
    cin >> n;
	
    vector < int > a(n + 1);
    for (int i = 1; i <= n; ++i) 
        cin >> a[i];
    
    vector < int > st(4 * n + 1);
    build_tree(1, 1, n, st, a);
	
    int q;
    cin >> q;
    while (q--) 
    {
        int type, x, y;
        cin >> type >> x >> y;
        
        // Gán giá trị y cho phần tử ở vị trí x.
        if (type == 1) 
            update(1, 1, n, x, y, st); 
        else // In ra giá trị nhỏ nhất trong đoạn [x, y].
            cout << get(1, 1, n, x, y, st) << '\n'; 
    }
}

6. Đánh giá độ phức tạp

Bộ nhớ

Xét hai trường hợp:

• TH1: $n = 2^k$: Cây phân đoạn đầy đủ, ở độ sâu cuối cùng có đúng $2^k$ lá, và các độ sâu thấp hơn không có nút lá nào (và các nút này đều có đúng $2$ con). Như vậy:

  • Tầng $k$: có $2^k$ nút.
  • Tầng $k−1$: có $2^{k−1}$ nút.
  • $...$

  $\Rightarrow$ Tổng số nút không quá $2k+1$ (vì tổng số nút là $2^k+2^{k−1} + \cdots +2^0 = 2^{k+1}−1$ theo công thức cấp số nhân).

• TH2: Với $n>2k$ và $n<2k+1$: Số nút của cây phân đoạn này không vượt quá số nút của cây phân đoạn với $n=2^{k+1}$.

Do đó, số nút của cây cho dãy $n$ phần tử (với $n≤2^k$) là không quá $2^{k+1},$ giá trị này xấp xỉ $4×n$. Bằng thực nghiệm, ta thấy dùng $4×n$ là đủ để lưu trữ dữ liệu trên cây. Vì vậy, trong cài đặt ở trên các bạn thấy người viết đã tạo ra một vector kích thước $4 \times n + 1$ để lưu trữ thông tin các nút của cây.

Thao tác xây dựng

Thao tác xây dựng sẽ yêu cầu một số lượng hoạt động không đổi trên mỗi nút của cây phân đoạn. Với mảng có $n$ phần tử thì số lượng nút của cây phân đoạn xấp xỉ $4×n$ (đã chứng minh ở trên), và vì thao tác xây dựng mất thời gian tuyến tính nên sẽ có độ phức tạp là $O(4×n)$.

Ta có thể nhận thấy rằng thao tác xây dựng nhanh hơn so với việc thực hiện các thao tác cập nhật riêng biệt (việc duyệt từng phần tử của mảng để cập nhật sẽ mất độ phức tạp $O\big(n × \log n)\big)$.

Thao tác cập nhật

Với thao tác cập nhật, một số lượng các hoạt động không đổi được thực hiện cho mỗi nút trên đường đi đơn từ gốc đến nút lá tương ứng với phần tử cần sửa đổi. Đồng nghĩa với việc ở mỗi độ sâu của cây, ta chỉ gọi đệ quy tới không quá 1 nút con.

Phân tích đoạn code trên, ta xét các trường hợp:

• Phần tử cần xét không nằm trong đoạn $[l,r]$ do nút $id$ quản lý. Trường hợp này ta dừng lại, không xét tiếp.
• Phần tử cần xét nằm trong đoạn $[l,r]$ do nút $id$ quản lý. Ta xét các con của nút $id$. Tuy nhiên chỉ có $1$ con của nút $id$ chứa phần tử cần xét và ta sẽ phải xét tiếp các con của nút này. Với nút con còn lại, ta sẽ dừng ngay mà không xét các con của nó nữa.

Vì số lượng các nút trên đường đi đơn từ gốc đến nút lá tương ứng được giới hạn bởi chiều cao của cây là $O(\log n)$ nên độ phức tạp của thao tác cập nhật sẽ là $O(\log n)$.

Thao tác lấy giá trị

Trước tiên, ta hãy xem xét từng độ sâu của của cây. Từ đó có thể thấy rằng đối với mỗi độ sâu, ta chỉ truy cập không quá $4$ nút. Và vì chiều cao của cây là $O(\log n)$ nên độ phức tạp của thao tác lấy giá trị là $O(\log n)$.

Ta có thể chứng minh rằng mệnh đề này (truy cập nhiều nhất bốn nút trong mỗi độ sâu) là đúng bằng phương pháp quy nạp:

• Ở độ sâu đầu tiên, ta chỉ truy cập duy nhất một nút là nút gốc, vì vậy ở đây ta truy cập ít hơn $4$ nút.
• Bây giờ, ta hãy xem xét một độ sâu bất kì. Theo giả thuyết quy nạp là ta thăm nhiều nhất $4$ nút. Nếu ta chỉ thăm nhiều nhất $2$ nút, thì ở độ sâu tiếp theo, số lượng nút được thăm nhiều nhất sẽ là $4$ nút. Điều đó thật hiển nhiên, bởi vì mỗi nút có thể tạo ra nhiều nhất $2$ lệnh gọi đệ quy.
• Vì vậy, giả sử rằng ta truy cập $3$ hoặc $4$ nút trong độ sâu hiện tại. Từ các nút đó, ta sẽ phân tích kỹ hơn các nút nằm ở giữa (nghĩa là nút thứ hai từ trái sang với số lượng nút đang được truy cập là $3$ và nút thứ $2, 3$ với số nút đang được truy cập là $4$). Vì truy vấn yêu cầu lấy giá trị của một đoạn con liên tục, ta biết rằng các phân đoạn tương ứng với các nút đã thăm ở giữa sẽ được bao phủ hoàn toàn bởi phân đoạn của truy vấn. Do đó các nút này sẽ không thực hiện bất kỳ lệnh gọi đệ quy nào tới các nút con nữa. Vì vậy, chỉ nút bên trái nhất và nút bên phải nhất mới có khả năng tiếp tục gọi đệ quy. Và hai nút đó sẽ chỉ tạo ra nhiều nhất $4$ lệnh gọi đệ quy, vì vậy độ sâu tiếp theo cũng sẽ đáp ứng đúng mệnh đề.

Do đó, ta sẽ chỉ truy cập nhiều nhất $4× \log n$ nút trên cây phân đoạn, và đó cũng chính là độ phức tạp của thao tác lấy giá trị!

III. Tổng kết

Như vậy, trong bài viết vừa rồi, chúng ta đã cùng tìm hiểu những vấn đề cơ bản của cấu trúc dữ liệu Cây phân đoạn - hay còn gọi là Segment Tree và áp dụng nó vào giải quyết một bài toán cụ thể, đó là bài toán RMQ.

Tuy nhiên, đó chưa phải là toàn bộ kiến thức về cấu trúc dữ liệu thú vị này. Trong các phần tiếp theo của series, chúng ta sẽ cùng nghiên cứu một số bài tập ví dụ để áp dụng Cây phân đoạn, và sau đó là phát triển một phương pháp cập nhật tốt hơn trên cây, nếu như bài toán phát sinh yêu câu cập nhật một đoạn. Hãy cùng theo dõi trong các bài viết tiếp theo về chủ đề Cây phân đoạn!

IV. Tài liệu tham khảo

• https://cp-algorithms.com/data_structures/segment_tree.html
• Tài liệu giáo khoa chuyên Tin quyển 2 - Thầy Hồ Sĩ Đàm.
• https://vnoi.info/wiki/algo/data-structures/segment-tree-basic.md
• Competitive Programming 3 - Steven Halim & Felix Halim.