Cách đo lường Bias và Variance bằng Bootstrap
Mục tiêu
Đo lường Bias và Variance của một mô hình Machine Learning bằng cách sử dụng Bootstrap Sampling.
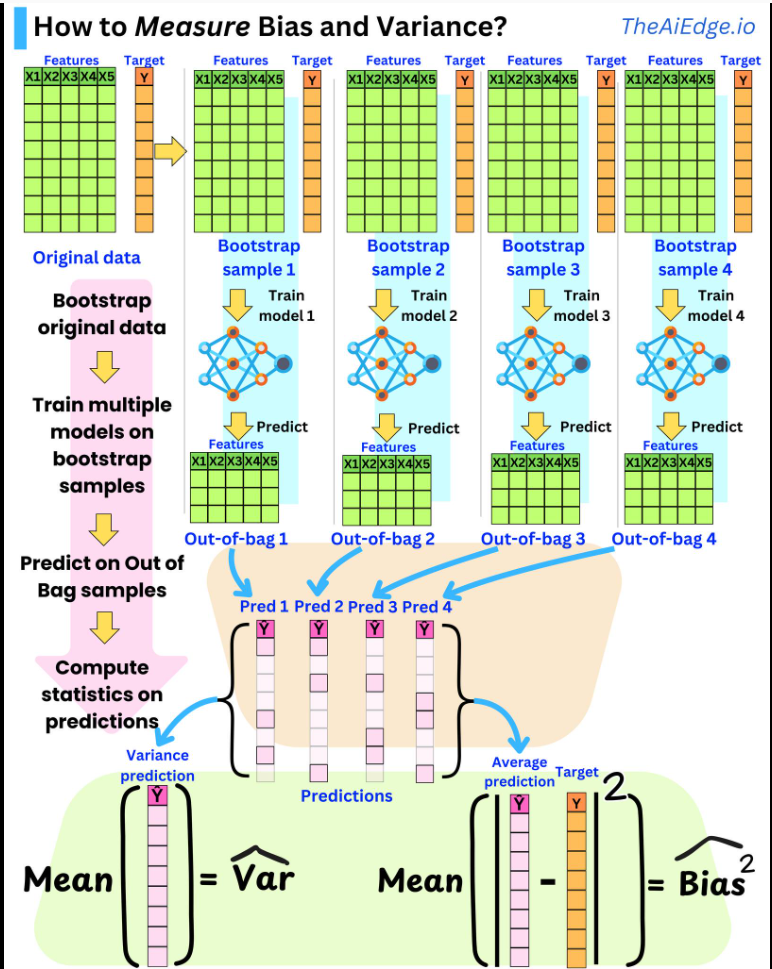
Bối cảnh
- Dữ liệu: Dataset có 5 đặc trưng (X1-X5) và 1 biến mục tiêu (Y).
- Mô hình: Ví dụ sử dụng mô hình đơn giản như Decision Tree, Neural Network nhỏ, hoặc bất kỳ model nào bạn muốn kiểm tra.
Các bước chi tiết
📊 Bước 1: Chuẩn bị dữ liệu gốc
Giả sử chúng ta có dataset với N = 100 dòng:
| X1 | X2 | X3 | X4 | X5 | Y |
|---|---|---|---|---|---|
| 0.5 | 1.2 | 0.3 | 1.5 | 2.3 | 10 |
| ... | ... | ... | ... | ... | ... |
Ký hiệu:
- D: Dataset gốc
- n: Số mẫu trong dataset (100)
🔁 Bước 2: Bootstrap Sampling
Sinh B mẫu bootstrap (ví dụ B = 4):
-
Với mỗi mẫu bootstrap b (b = 1 → 4)
- Lấy mẫu ngẫu nhiên n dòng từ D với hoàn lại (sampling with replacement).
- Phần dữ liệu không được chọn sẽ được gọi là Out-of-Bag (OOB) cho sample đó.
Giả sử:
| Bootstrap sample | Size | Out-of-Bag size |
|---|---|---|
| Sample 1 | 100 | 30 |
| Sample 2 | 100 | 28 |
| Sample 3 | 100 | 27 |
| Sample 4 | 100 | 31 |
🛠️ Bước 3: Train mô hình trên từng mẫu bootstrap
- Với mỗi bootstrap sample b, train một mô hình M_b.
Ví dụ:
- Model 1 → train trên Sample 1
- Model 2 → train trên Sample 2
- v.v.
🔮 Bước 4: Dự đoán trên Out-of-Bag (OOB) samples
- Với mỗi mô hình M_b, dự đoán Ŷ_b trên Out-of-Bag sample tương ứng.
- Lưu lại dự đoán cho từng điểm dữ liệu nằm trong OOB.
Giả sử điểm dữ liệu i = 5 (Y = 15) có 2 model mà nó nằm trong OOB:
| Model | Predicted value (Ŷ) |
|---|---|
| Model 1 | 14 |
| Model 3 | 16 |
🧮 Bước 5: Tính thống kê trên dự đoán
-
Với mỗi điểm dữ liệu i (có ít nhất một OOB prediction):
- Tính Mean Prediction (trung bình các giá trị dự đoán)
- Tính Variance (độ biến thiên giữa các prediction)
- Tính Bias squared bằng công thức:
Ví dụ cho điểm i = 5:
- Predictions: [14,16]
- MeanPrediction = (14+16)/2 = 15
- TrueY = 15
- Bias² = (15 - 15)^2 = 0
- Variance = Var([14,16]) = ((14 - 15)^2 + (16 - 15)^2)/2 = (1 + 1)/2 = 1
📈 Bước 6: Tổng hợp kết quả toàn dataset
-
Lặp lại bước 5 cho toàn bộ điểm dữ liệu có dự đoán OOB.
-
Cuối cùng tính:
- Mean Bias² (trung bình tất cả Bias²)
- Mean Variance (trung bình tất cả Variance)
Công thức tổng thể:
✅ Kết luận
Bạn sẽ có được:
- Bias thể hiện mức độ sai lệch trung bình của mô hình.
- Variance thể hiện độ dao động của dự đoán mô hình khi thay đổi dữ liệu huấn luyện.
All rights reserved